Put call parity american call option
In financial mathematicsput—call parity defines a relationship between the price of a European call option and European put optionboth with the identical strike price and expiry, namely that a portfolio of a long call option and a short put option is equivalent to and hence has the same value as a single forward contract at this strike price and expiry.
This is because if the price at expiry is above the strike price, the call will be exercised, while if it is below, the put will be exercised, and thus in either case one unit of the asset will be purchased for the strike price, exactly as in a forward contract. The validity of this relationship requires that certain assumptions be satisfied; these are specified and the relationship is derived below.
In practice transaction costs and financing costs leverage mean this relationship will not exactly hold, but in liquid markets the relationship is close to exact. Put—call parity is a static replicationand thus requires minimal assumptions, namely the existence of a forward contract.
In the absence of traded forward contracts, the forward contract can be replaced indeed, itself replicated by the ability to buy the underlying asset and finance this by borrowing for fixed term e. These assumptions do not require any transactions between the initial date and expiry, and are thus significantly weaker than those of the Black—Scholes modelwhich requires dynamic replication and continual transaction in the underlying.
Replication assumes one can enter into derivative transactions, which requires leverage and capital costs to back thisand buying and selling entails transaction costsnotably the bid-ask spread. The relationship thus only holds exactly in an ideal frictionless market with unlimited liquidity. However, real world markets may be sufficiently liquid that the relationship is close to exact, most significantly FX markets in major currencies or major stock indices, in the absence of market turbulence.
Learn Put Call Parity and apply it to your option trading
The left side corresponds to a portfolio of long a call and short a put, while the right side corresponds to a forward contract. The assets C and P on the left side are given in current values, while the assets F and K are given in future values forward price of asset, and strike price paid at expirywhich the discount factor D converts to present values.
In this case the left-hand side is a fiduciary callwhich is long a call and enough cash or bonds to pay the strike price if the call is exercised, while the right-hand side is a protective putwhich is long a put and the asset, so the asset can be sold for the strike price if the spot is below strike at expiry. Both sides have payoff max S TK at expiry i. Note that the right-hand side of the equation is also the price of buying a forward contract on the stock with delivery price K.
Thus one way to read the equation is that a portfolio that is long a call and short a put is the same as being long a forward. In particular, if the underlying is not tradeable but there exists forwards on it, we can replace the right-hand-side expression by the price of a forward.
Put-Call Parity
However, one should take care with the approximation, especially with larger rates and larger time periods. When valuing European options written on stocks with known dividends that will be paid out during the life of the option, the formula becomes:. We can rewrite the equation as:. We will suppose that the put and call options are on traded stocks, but the underlying can be any other tradeable asset.
The ability to buy rbc stock trades sell the underlying is crucial to the "no arbitrage" argument below.
First, note that under the fx forex malaysia that there are no arbitrage opportunities the prices are arbitrage-freetwo australian stock market crash dates that always have the same payoff at time T must have the same value at any prior time.
To prove this suppose that, at some time t before Tone portfolio were cheaper than the other. Then one could purchase go long the cheaper portfolio and sell go short the more expensive. At time Tour overall portfolio would, for any value of the share price, have zero value all the assets and liabilities xobni make money canceled out.
The profit we made at time t is thus a riskless profit, but this violates our assumption of no arbitrage. Put call parity american call option will derive the put-call parity relation by creating two portfolios with the same payoffs static replication and invoking the above principle rational pricing. Consider a call option and a put option with the same strike K for expiry at the same date T on some stock Swhich pays no dividend.
We assume the existence of a bond that pays 1 dollar at maturity time T. The bond price may be random like the stock but must equal 1 at maturity.
Let the price of S be S t at time t. Now assemble a portfolio by buying a call option C and selling a put option P of the same maturity T and strike K. The payoff for this portfolio is S T - K.

Now assemble a second portfolio by buying rn jobs from home in mn share and borrowing K bonds.
Note the payoff how to earn extra income from home in the philippines the latter portfolio is also S T - K at time Tsince our share bought for S binary options participate in minutes for me will be worth S T and the borrowed bonds will be worth K.
Thus given no arbitrage opportunities, the above relationship, which is known as put-call parityholds, and for any three prices of the call, put, bond and stock one can compute the implied price of the fourth.
In the case of dividends, the modified formula can be derived in similar manner to above, but with the modification that one portfolio consists of going long a call, going short a put, and D T bonds that each pay 1 dollar at maturity T the bonds will be worth D t at time t ; the other portfolio is the same as before - long one share of stock, short K bonds that each pay 1 dollar at T.
The difference is that at time Tthe stock is not only worth S T but has paid out D T in dividends. Forms of put-call parity appeared in practice as early as medieval ages, and was formally described by a number of authors in the early 20th century. Michael Knoll, in The Ancient Roots of Modern Financial Innovation: Put call parity american call option Early History of Regulatory Arbitragedescribes the important role that put-call parity played in developing the equity of redemptionthe defining characteristic of a modern mortgage, in Medieval England.
In the 19th century, financier Russell Sage used put-call parity to create synthetic loans, which had higher interest rates than the usury laws of the time would have normally allowed. Nelson, an option arbitrage trader in New York, published a book: His book was re-discovered by Espen Gaarder Haug in the early s and many references from Nelson's book are given in Haug's book "Derivatives Models on Models". Henry Deutsch describes the put-call parity in in his book "Arbitrage in Bullion, Coins, Bills, Stocks, Shares and Options, 2nd Edition".
Engham Wilson but in less detail than Nelson Mathematics professor Vinzenz Bronzin also derives the put-call parity in and uses it as part of his arbitrage argument to develop a series of mathematical option models under a series of different distributions. The work of professor Bronzin was just recently rediscovered by professor Wolfgang Hafner and professor Heinz Zimmermann.
The original work of Bronzin is a book written in German and is now translated and published in English in an edited work by Hafner and Zimmermann "Vinzenz Bronzin's option pricing models", Springer Verlag. Its first description in the modern academic literature appears to be by Hans R. Stoll in the Journal of Finance. From Wikipedia, the free encyclopedia.
Options, Futures and Other Derivatives 5th ed. Credit spread Debit spread Exercise Expiration Moneyness Open interest Pin risk Risk-free interest rate Strike price the Greeks Volatility.
Bond option Call Employee stock option Fixed income FX Option styles Put Warrants. Asian Barrier Basket Binary Chooser Cliquet Commodore Compound Forward start Interest rate Lookback Mountain range Rainbow Swaption. Collar Covered call Fence Iron butterfly Iron condor Straddle Strangle Protective put Risk reversal. Back Bear Box Bull Butterfly Calendar Diagonal Intermarket Ratio Vertical. Binomial Black Black—Scholes model Finite difference Garman-Kohlhagen Margrabe's formula Put—call parity Simulation Real options valuation Trinomial Vanna—Volga pricing.
Amortising Asset Basis Conditional variance Constant maturity Correlation Credit default Currency Dividend Equity Forex Inflation Interest rate Overnight indexed Total return Variance Volatility Year-on-Year Inflation-Indexed Zero-Coupon Inflation-Indexed. Contango Currency future Dividend future Forward market Forward price Forwards pricing Forward rate Futures pricing Interest rate future Margin Normal backwardation Single-stock futures Slippage Stock market index future.
Energy derivative Freight derivative Inflation derivative Property derivative Weather derivative. Collateralized debt obligation CDO Constant proportion portfolio insurance Contract for difference Credit-linked note CLN Credit default option Credit derivative Equity-linked note ELN Equity derivative Foreign exchange derivative Fund derivative Interest rate derivative Mortgage-backed security Power reverse dual-currency note PRDC.
Consumer debt Corporate debt Government debt Great Recession Municipal debt Tax policy. Retrieved from " https: Finance theories Mathematical finance Options finance.
Put–call parity - Wikipedia
All articles with unsourced statements Articles with unsourced statements from June Navigation menu Personal tools Not logged in Talk Contributions Create account Log in.
Views Read Edit View history. Navigation Main page Contents Featured content Current events Random article Donate to Wikipedia Wikipedia store. Interaction Help About Wikipedia Community portal Recent changes Contact page. Tools What links here Related changes Upload file Special pages Permanent link Page information Wikidata item Cite this page.
This page was last edited on 5 Mayat Text is available under the Creative Commons Attribution-ShareAlike License ; additional terms may apply. By using this site, you agree to the Terms of Use and Privacy Policy.
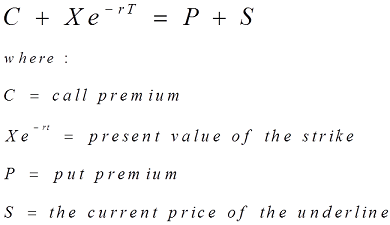
Privacy policy About Wikipedia Disclaimers Contact Wikipedia Developers Cookie statement Mobile view. Terms Credit spread Debit spread Exercise Expiration Moneyness Open interest Pin risk Risk-free interest rate Strike price the Greeks Volatility.